Скалярные и векторные физические величины

Все физические величины можно разделить на два фундаментальных типа: скалярные (рис.1) и векторные (рис.2). Ключевое различие между ними — наличие направления.

Скалярные величины

Характеризуются только числовым значением (модулем) и не имеют направления.

Примеры скалярных величин:

Масса (m)
Объём (V)
Время (t)
Путь (S)
Работа (A)
Давление (P)
Электрический заряд (q)
Сила тока (I)
Температура (T)

Важно: Скалярные величины можно складывать и умножать обычным алгебраическим способом.

Векторные величины

Характеризуются числовым значением (модулем) и направлением в пространстве.

Примеры векторов:

Скорость (v)
Ускорение (a)
Перемещение (s)
Сила (F)
Импульс (p)
Напряженность электрического поля (E)

Важно: Для сложения и вычитания векторов необходимы специальные методы (правило треугольника или параллелограмма).

Сравнительная таблица

Характеристика	Скалярная величина	Векторная величина
Определение	Задаётся только числом (модулем)	Задаётся числом (модулем) и направлением
Сложение	Алгебраическое	Геометрическое (по правилу параллелограмма или треугольника)
Пример	Масса 5 кг	Скорость 5 м/с, на север

Вектор

Что такое вектор?

Вектор — это направленный отрезок, который характеризуется длиной (модулем) и направлением в пространстве.

Обозначения векторов

Векторные величины обозначаются буквой со стрелкой:F, p, a
Длина вектора (модуль) обозначается без стрелки:F, p, a
Или через обозначение модуля:|F|, |p|,|a|

Правила записи

F = 5 Н (модуль вектора)

|F| = 5 Н (модуль вектора)

F = 5 Н — НЕВЕРНО

Равенство векторов

Два вектора называются равными, если они:

Имеют одинаковую длину (модуль)
Сонаправлены (имеют одинаковое направление)

Примечание: Равные векторы могут находиться в разных точках пространства — важно лишь их направление и длина.

Дополнительная информация

Нулевой вектор — это вектор с нулевой длиной (модулем). Обозначается 0. Не имеет определенного направления.

Противоположные векторы

Противоположные векторы — это векторы, имеющие одинаковую длину, но противоположно направленные. Если a — вектор, то -a — противоположный ему.

Сложение векторов

Основы сложения векторов

Пусть даны два произвольных вектора F₁ и F₂. Для сложения векторов используются два основных метода: правило параллелограмма и правило треугольника.

Правило параллелограмма

Совместите начала векторов F₁ и F₂ параллельным переносом
Постройте на этих векторах параллелограмм (как на сторонах)
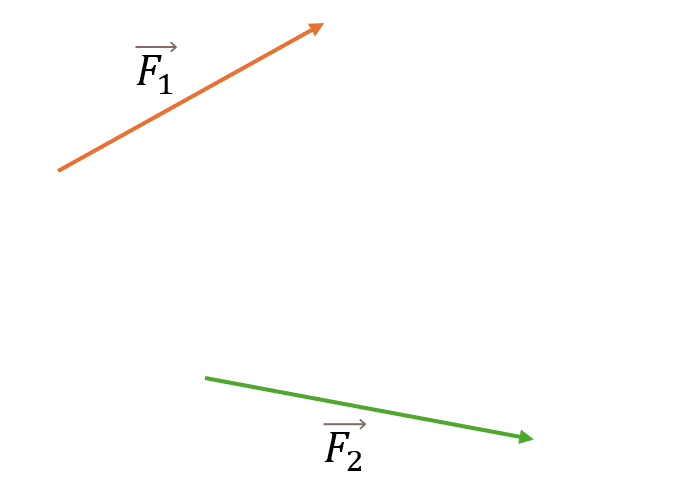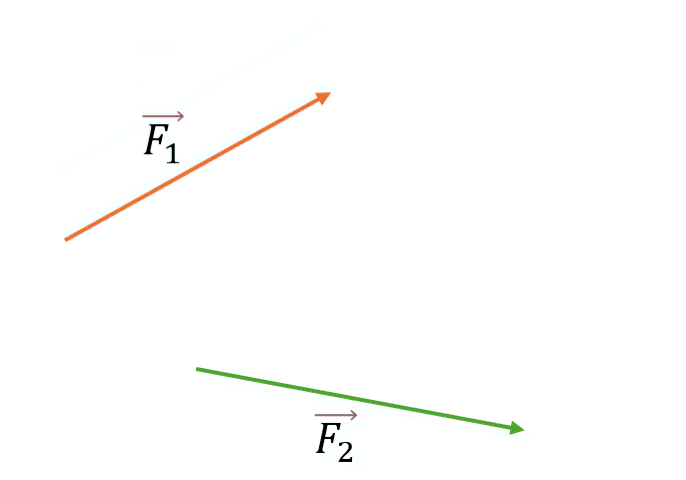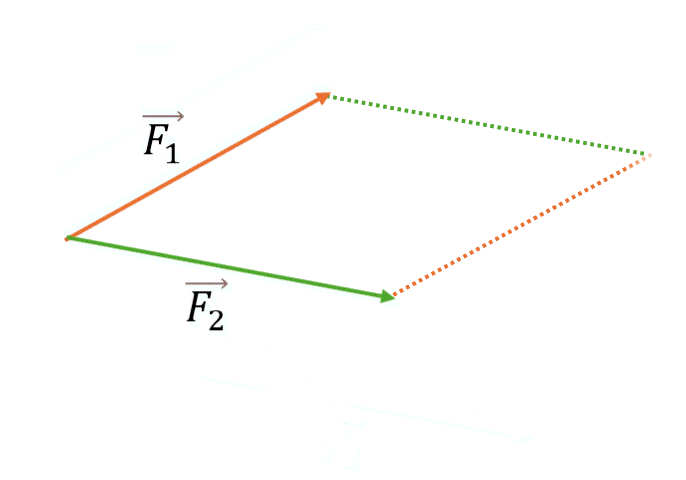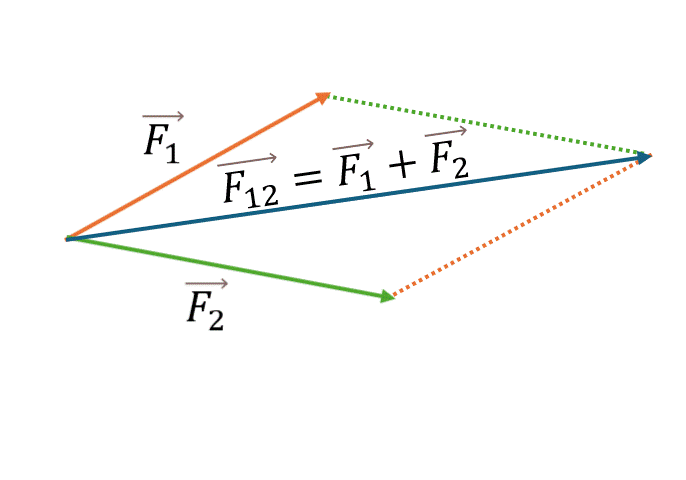
Проведите диагональ из общего начала векторов
Эта диагональ представляет собой сумму векторов F₁₂ = F₁ + F₂

Особенность: Правило параллелограмма особенно удобно, когда векторы выходят из одной точки.

Правило треугольника

Отложите вектор F₁
К концу вектора F₁ приложите начало вектора F₂ (параллельным переносом)
Проведите вектор из начала F₁ в конец F₂
Этот вектор представляет собой сумму F₁₂ = F₁ + F₂

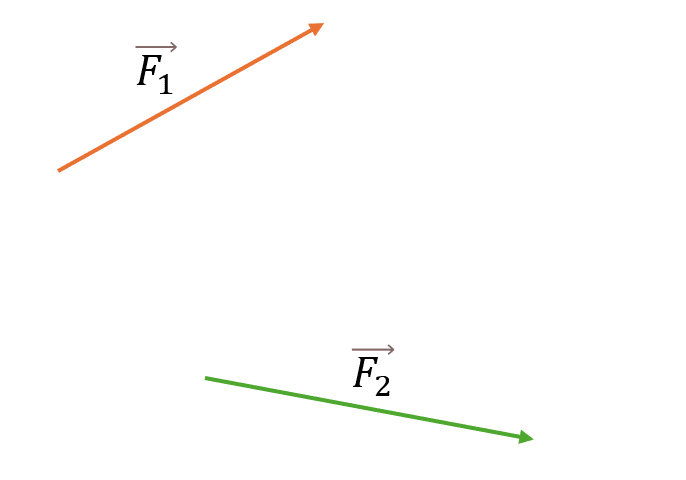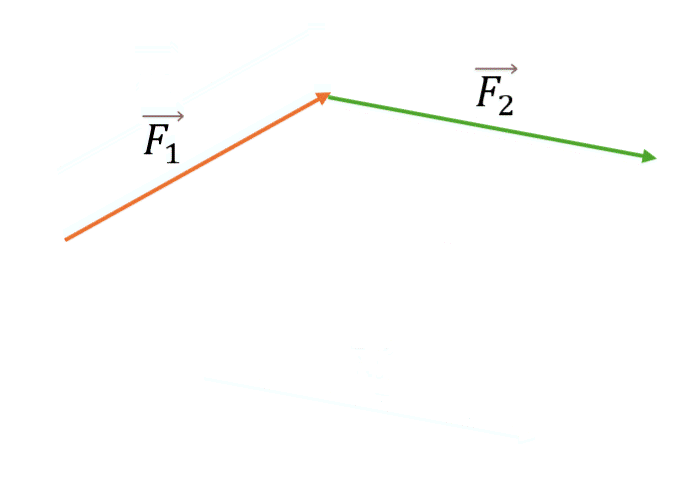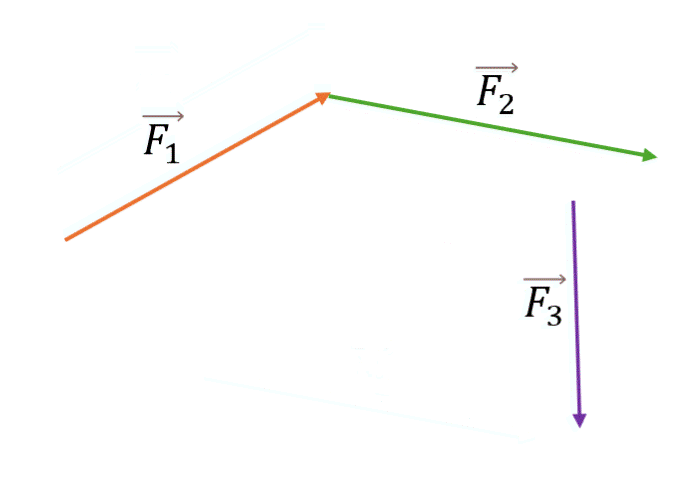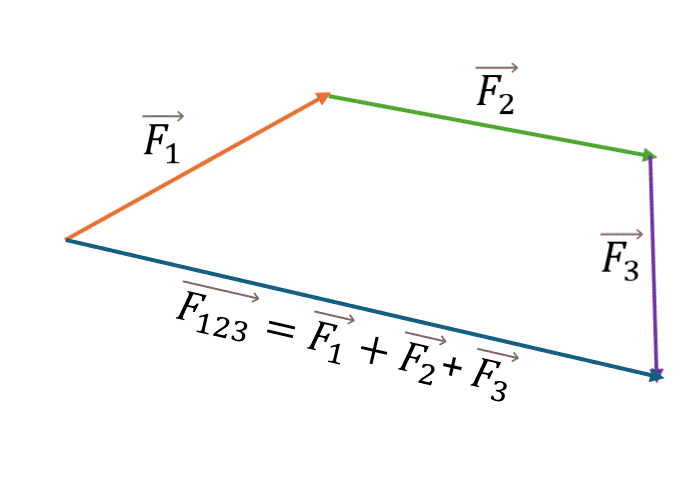
Особенность: Правило треугольника удобно для последовательного сложения нескольких векторов.

Правило параллелограмма: анимация показывающая построение параллелограмма и его диагонали — Рис. 3. Правило параллелограмма

Правило треугольника: анимация показывающая последовательное сложение векторов — Рис. 4. Правило треугольника

Сравнение методов сложения

Критерий	Правило параллелограмма	Правило треугольника
Лучше для	Сложения двух векторов	Сложения трёх и более векторов
Условие применения	Векторы выходят из одной точки	Векторы соединены последовательно
Визуализация	Диагональ параллелограмма	Замыкающая ломаная линия

Свойства сложения векторов

Коммутативность

a + b = b + a
От перемены мест слагаемых сумма не меняется

Ассоциативность

(a + b) + c = a + (b + c)
Результат не зависит от порядка сложения

Практический совет

При сложении двух векторов предпочтительнее использовать правило параллелограмма. Когда же речь идет о нахождении суммы трёх и более векторов, лучше последовательно использовать правило треугольника.

Проекция вектора на заданное направление

Что такое проекция вектора?

Пусть заданы два вектора a и b. Проекцией вектора a на направление вектора b называется скалярная величина, равная длине отрезка, образованного перпендикулярными проекциями начала и конца вектора a на прямую, содержащую вектор b.

Математическое определение

a_b = |\vec{a}| \cdot \cos\alpha = a \cdot \cos\alpha

где:

a_b — проекция вектора a на направление b
a — модуль (длина) вектора a
α — угол между векторами a и b

Свойства проекции

Проекция — величина алгебраическая (число, которое может быть положительным или отрицательным) или геометрическая (проекция вектора на ось как вектор)
Проекция положительна, если угол α острый (0° ≤ α < 90°)
Проекция отрицательна, если угол α тупой (90° < α ≤ 180°)
Проекция равна нулю, если векторы перпендикулярны (α = 90°)
Проекция равна модулю вектора, если векторы сонаправлены (α = 0°)

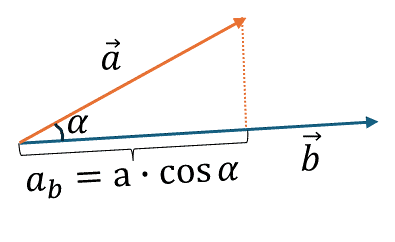
Проекция вектора а на b: графическое представление с обозначением угла α между векторами — Рис. 5. Проекция вектора а на вектор b

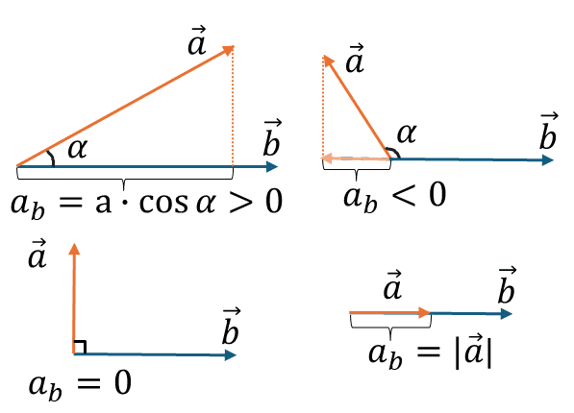
Примеры положительных и отрицательных проекций векторов в зависимости от угла — Рис. 6. Знаки проекций в зависимости от угла

Проекция на координатные оси

В физике часто необходимо находить проекции векторов на координатные оси заданной системы отсчёта.

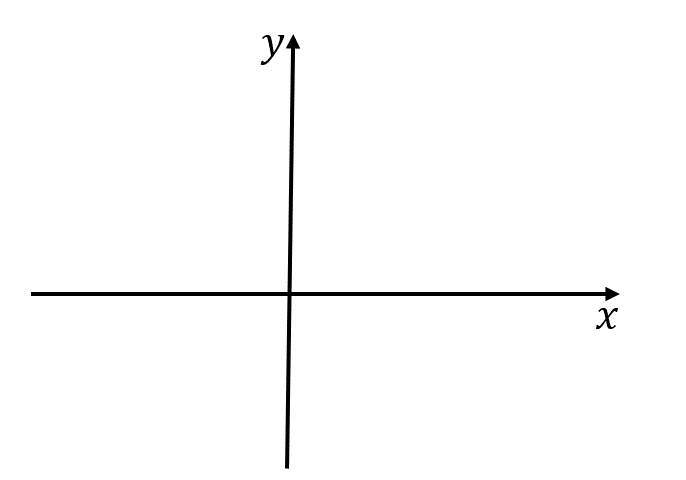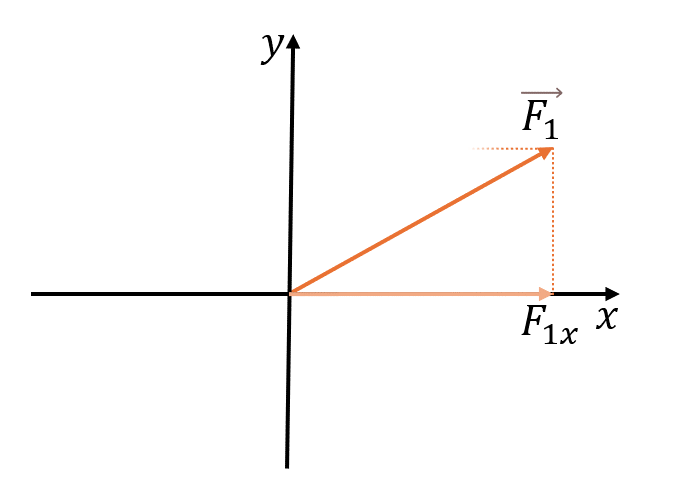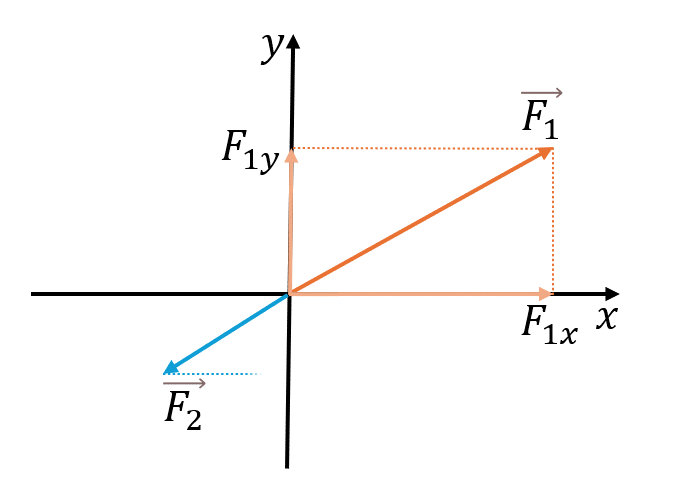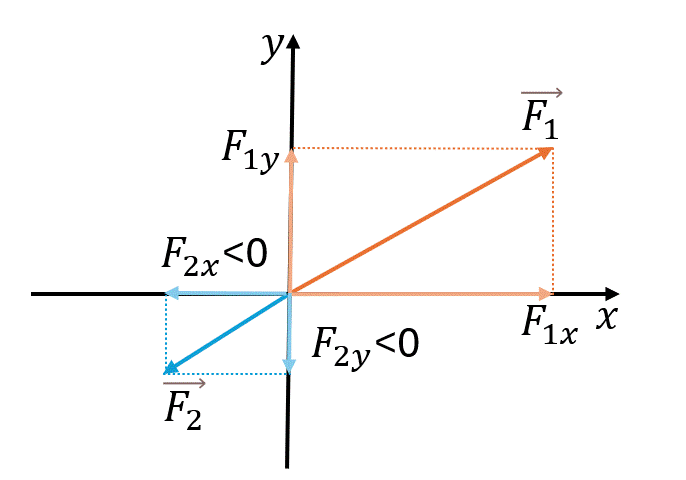
Двумерная система (XOY)

F_x = F \cdot \cos\alpha

F_y = F \cdot \sin\alpha = F \cdot \cos\beta

где α — угол между вектором F и осью OX,
β — угол между вектором F и осью OY

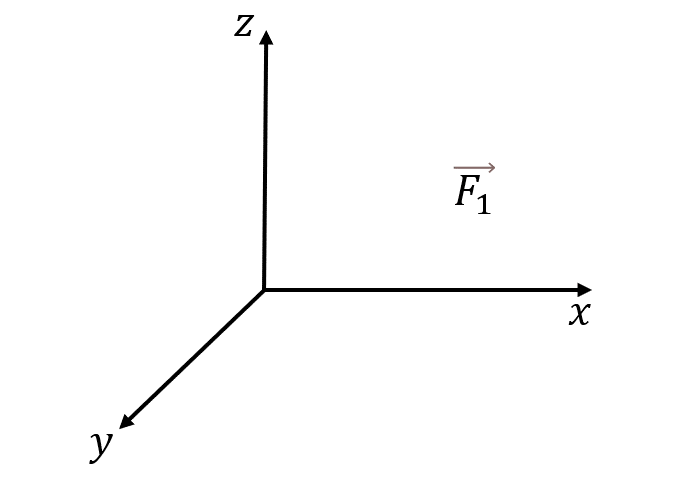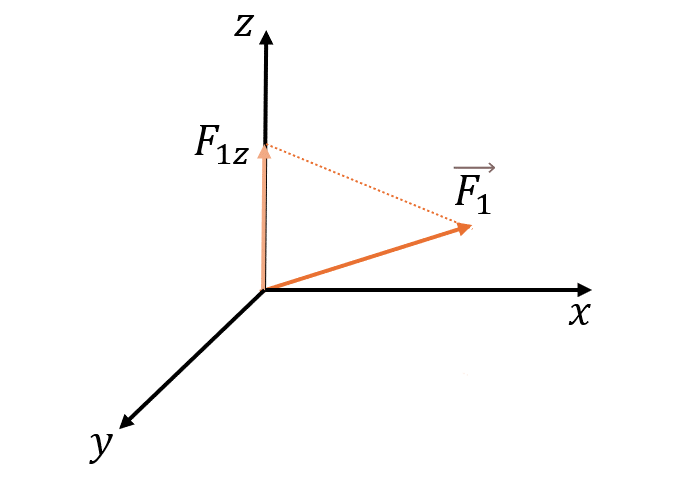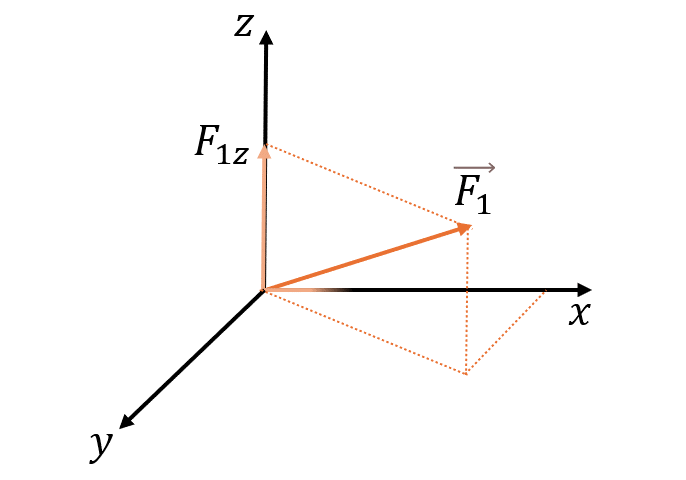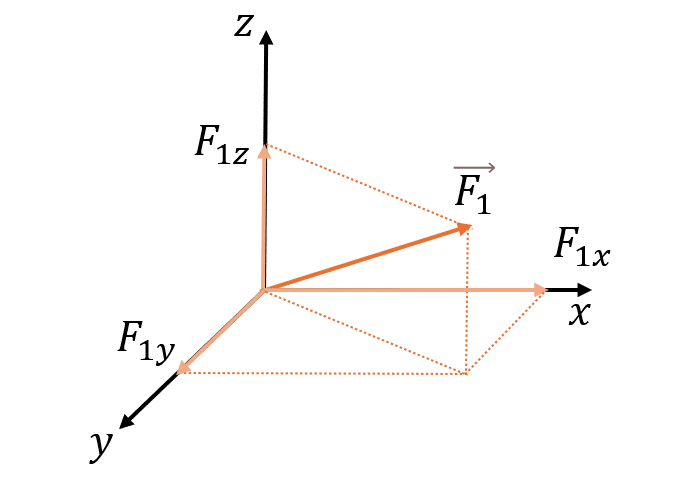
Трёхмерная система (XYZ)

F_x = F \cdot \cos\alpha

F_y = F \cdot \cos\beta

F_z = F \cdot \cos\gamma

где α, β, γ — углы между вектором Fи осями OX, OY и OZ соответственно

Анимация процесса нахождения проекций вектора на оси OX и OY в двумерной системе координат — Рис. 7. Двумерная система отсчёта

Анимация процесса нахождения проекций вектора на оси OX, OY и OZ в трёхмерной системе координат — Рис. 8. Трёхмерная система отсчёта

Практическое применение

Проекции векторов широко используются в физике для:

Решения задач на равновесие тел
Анализа движения под углом к горизонту
Расчёта работы силы (как проекции силы на направление перемещения)
Определения момента силы
Разложения сил на составляющие

Важное замечание

При вычислении проекций важно правильно определить углы между вектором и осями координат. В трехмерном пространстве для этого используются направляющие косинусы, которые удовлетворяют соотношению:

\cos^2\alpha + \cos^2\beta + \cos^2\gamma = 1

Тригонометрия в физике: sin(α), cos(α), tg(α) и ctg(α)

Основы тригонометрии для физики

Для работы с векторами в физике необходимо уверенно владеть тригонометрическими функциями: синусом, косинусом, тангенсом и котангенсом. Эти функции позволяют находить проекции векторов, решать задачи на равновесие и анализировать различные физические процессы.

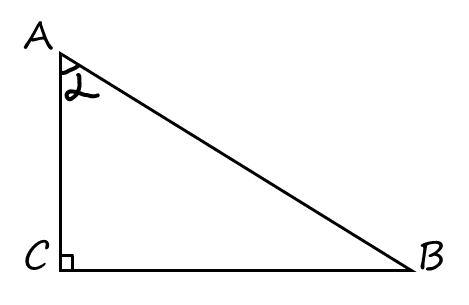
Прямоугольный треугольник

Рассмотрим прямоугольный треугольник ABC, где угол C = 90°, а α — острый угол при вершине A.

Стороны:

AB — гипотенуза (c)
BC — противолежащий катет (a)
AC — прилежащий катет (b)

Углы:

∠A = α
∠B = β
∠C = 90°

Прямоугольный треугольник с обозначением сторон и углов — Рис. 9. Прямоугольный треугольник

Тригонометрические функции

Синус и косинус

Синус острого угла — отношение противолежащего катета к гипотенузе:

\sin\alpha = \frac{a}{c} = \frac{BC}{AB}

Косинус острого угла — отношение прилежащего катета к гипотенузе:

\cos\alpha = \frac{b}{c} = \frac{AC}{AB}

Тангенс и котангенс

Тангенс острого угла — отношение противолежащего катета к прилежащему:

\tg\alpha = \frac{a}{b} = \frac{BC}{AC}

Котангенс острого угла — отношение прилежащего катета к противолежащему:

\ctg\alpha = \frac{b}{a} = \frac{AC}{BC}

Связь между тригонометрическими функциями

\tg\alpha = \frac{\sin\alpha}{\cos\alpha}

\ctg\alpha = \frac{\cos\alpha}{\sin\alpha} = \frac{1}{\tg\alpha}

\sin^2\alpha + \cos^2\alpha = 1

1 + \tg^2\alpha = \frac{1}{\cos^2\alpha}

Основные теоремы геометрии

Для решения физических задач также необходимы знания основных геометрических теорем.

Теорема Пифагора

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов:

c^2 = a^2 + b^2

где c — гипотенуза, a и b — катеты прямоугольного треугольника.

Теорема синусов

Отношение сторон треугольника к синусам противолежащих углов равно диаметру описанной окружности:

\frac{a}{\sin\alpha} = \frac{b}{\sin\beta} = \frac{c}{\sin\gamma} = 2R

где a, b, c — стороны треугольника; α, β, γ — противолежащие углы; R — радиус описанной окружности.

Теорема косинусов

Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:

a^2 = b^2 + c^2 - 2bc\cos\alpha

где a — сторона треугольника; b, c — другие стороны; α — угол между сторонами b и c.

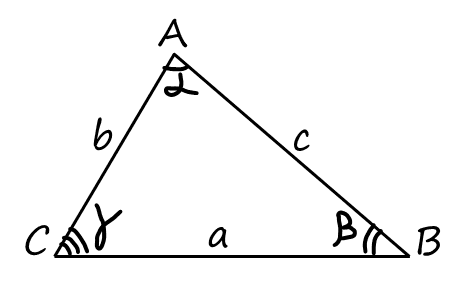
Произвольный треугольник с обозначением сторон и углов — Рис. 10. Произвольный треугольник

Таблица значений тригонометрических функций

Угол	sin	cos	tg	ctg
0°	0	1	0	∞
30° (π/6)	1/2	√3/2	√3/3	√3
45° (π/4)	√2/2	√2/2	1	1
60° (π/3)	√3/2	1/2	√3	√3/3
90° (π/2)	1	0	∞	0

Применение в физике

Тригонометрические функции широко применяются в различных разделах физики:

Нахождение проекций векторов на координатные оси
Решение задач на равновесие тел
Анализ гармонических колебаний
Расчет траекторий движения под углом к горизонту
Описание волновых процессов
Расчет работы силы при движении под углом

Разложение векторов на составляющие и базисные векторы

Основы разложения векторов

Любой вектор можно представить в виде суммы двух или более других векторов. Это преобразование называется разложением вектора и широко применяется при решении физических и геометрических задач, позволяя упростить сложные операции.

Базисные векторы

Базисные векторы — это особые векторы единичной длины, направленные вдоль координатных осей. Они образуют основу (базис) координатной системы.

В трехмерном пространстве:

$\vec{i}$ — единичный вектор вдоль оси X
$\vec{j}$ — единичный вектор вдоль оси Y
$\vec{k}$ — единичный вектор вдоль оси Z

Свойства базисных векторов: Все базисные векторы имеют длину 1, взаимно перпендикулярны и образуют правую тройку векторов.

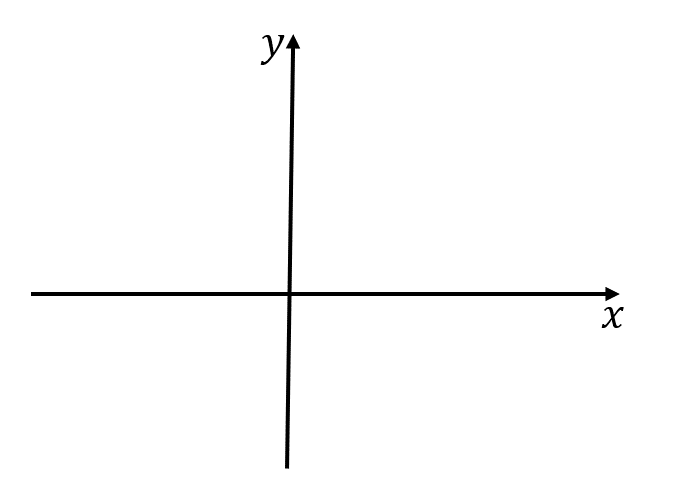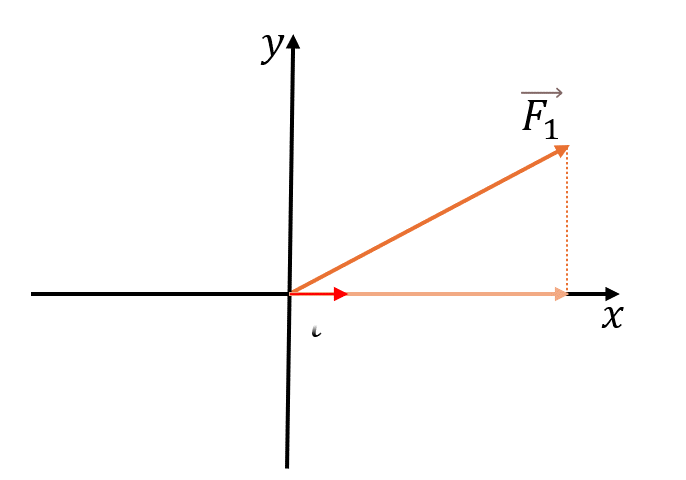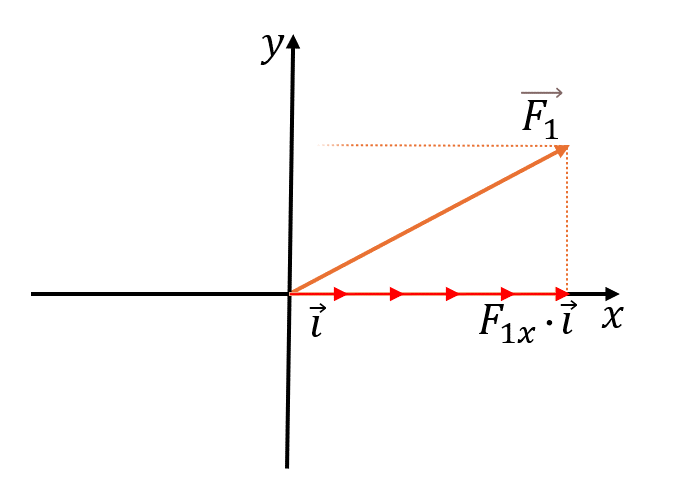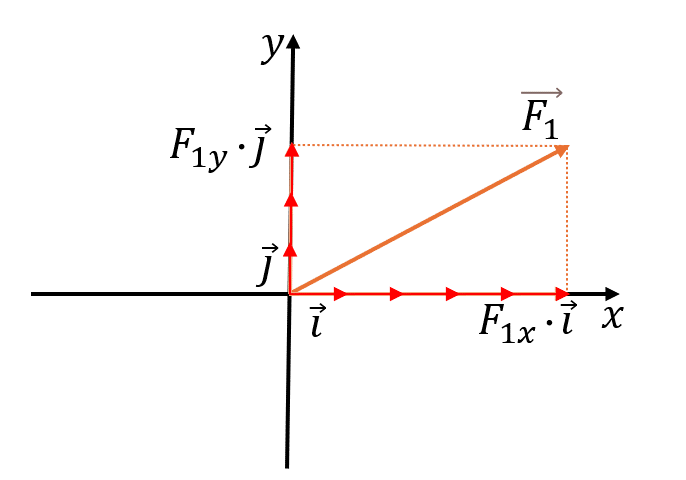
Формулы разложения

Разложение вектора:

\vec{F} = F_x\vec{i} + F_y\vec{j} + F_z\vec{k}

где $F_x, F_y, F_z$ — проекции вектора на соответствующие оси координат

Модуль вектора:

|\vec{F}| = \sqrt{F_x^2 + F_y^2 + F_z^2}

Визуализация разложения вектора на составляющие в двумерном пространстве — Рис. 11. Графическое представление разложения вектора на составляющие

Демонстрация разложения по базисным векторам в двумерной системе координат — Рис. 12. Разложение вектора по базисным векторам

Примеры разложения векторов

Двумерное пространство

В двумерном пространстве вектор раскладывается на две компоненты:

\vec{F} = F_x\vec{i} + F_y\vec{j}

Компоненты находятся через угол α между вектором и осью X:

F_x = |\vec{F}| \cos\alpha

F_y = |\vec{F}| \sin\alpha

Трехмерное пространство

В трехмерном пространстве вектор раскладывается на три компоненты:

\vec{F} = F_x\vec{i} + F_y\vec{j} + F_z\vec{k}

Компоненты находятся через направляющие косинусы:

F_x = |\vec{F}| \cos\alpha

F_y = |\vec{F}| \cos\beta

F_z = |\vec{F}| \cos\gamma

Практическое применение в физике

Преимущества разложения

Упрощение векторных операций (сложение, вычитание)
Возможность работы с проекциями вместо полных векторов
Упрощение решения систем уравнений
Возможность применения алгебраических методов

Примеры применения

Анализ сил в механике
Расчет напряженности электрического поля
Определение магнитной индукции
Решение задач кинематики
Расчет работы и энергии

Связь с координатами точек

Если вектор задан координатами начальной и конечной точек, его проекции можно найти как разности соответствующих координат:

\vec{AB} = (x_B - x_A)\vec{i} + (y_B - y_A)\vec{j} + (z_B - z_A)\vec{k}

\vec{AB} = (x_B - x_A)\vec{i} + (y_B - y_A)\vec{j} + (z_B - z_A)\vec{k}

где A(x₁, y₁, z₁) — начальная точка, B(x₂, y₂, z₂) — конечная точка вектора

Ортогональные и ортонормированные базисы

Ортогональный базис

Базисные векторы перпендикулярны друг другу, но могут иметь произвольную длину.

Ортонормированный базис

Базисные векторы перпендикулярны друг другу и имеют единичную длину. Именно такой базис используется чаще всего.

Важно: В ортонормированном базисе скалярное произведение базисных векторов равно нулю при разных индексах и единице при одинаковых: $\vec{i} \cdot \vec{j} = 0$ , $\vec{i} \cdot \vec{i} = 1$ .

Скалярное и векторное произведение векторов

Операции с векторами

Для работы с векторами в физике используются две основные операции умножения: скалярное произведение (результат - число) и векторное произведение (результат - вектор). Эти операции играют ключевую роль в различных разделах физики.

Скалярное произведение

Скалярным произведением двух векторов F₁ и F₂ называется число, равное произведению модулей этих векторов на косинус угла между ними.

Формулы:

\vec{F}_1 \cdot \vec{F}_2 = |\vec{F}_1| \cdot |\vec{F}_2| \cdot \cos\alpha

\vec{F}_1 \cdot \vec{F}_2 = F_{1x}F_{2x} + F_{1y}F_{2y} + F_{1z}F_{2z}

Свойства:

Коммутативно: a · b = b · a
Дистрибутивно: a · (b + c) = a · b + a · c
Если векторы перпендикулярны, скалярное произведение равно нулю

Векторное произведение

Векторным произведением двух векторов F₁ и F₂ называется вектор, перпендикулярный плоскости, содержащей эти векторы.

Формулы:

|\vec{F}_1 \times \vec{F}_2| = |\vec{F}_1| \cdot |\vec{F}_2| \cdot \sin\alpha

\vec{F}_1 \times \vec{F}_2 = \begin{vmatrix} \vec{i} & \vec{j} & \vec{k} \\ F_{1x} & F_{1y} & F_{1z} \\ F_{2x} & F_{2y} & F_{2z} \end{vmatrix}

Свойства:

Антикоммутативно: a × b = -b × a
Дистрибутивно: a × (b + c) = a × b + a × c
Если векторы параллельны, векторное произведение равно нулю

Визуализация скалярного произведения векторов — Рис. 13. Скалярное произведение векторов

Визуализация векторного произведения: анимация показывающая образование нового вектора, перпендикулярного исходным — Рис. 14. Векторное произведение векторов

Сравнение произведений векторов

Характеристика	Скалярное произведение	Векторное произведение
Результат	Скаляр (число)	Вектор
Обозначение	a · b	a × b
Коммутативность	Да	Нет (антикоммутативно)
Зависимость от угла	cos α	sin α
Максимальное значение	\|a\|·\|b\| (при α=0°)	\|a\|·\|b\| (при α=90°)
Нулевое значение	При α=90°	При α=0° или α=180°

Применение в физике

Скалярное произведение

Работа силы: A = F · s
Мощность: P = F · v
Поток векторного поля: Φ = E · S

Векторное произведение

Момент силы: M = r × F
Угловая скорость: v = ω × r
Момент импульса: L = r × p

Геометрическая интерпретация

Скалярное произведение

Скалярное произведение равно произведению модуля одного вектора на проекцию второго вектора на направление первого:

\vec{a} \cdot \vec{b} = |\vec{a}| \cdot |\vec{b}| \cdot \cos\alpha = |\vec{a}| \cdot \text{пр}_{\vec{a}}\vec{b}

\vec{a} \cdot \vec{b} = |\vec{a}| \cdot |\vec{b}| \cdot \cos\alpha = |\vec{a}| \cdot \text{пр}_{\vec{a}}\vec{b}

Векторное произведение

Модуль векторного произведения равен площади параллелограмма, построенного на этих векторах:

|\vec{a} \times \vec{b}| = |\vec{a}| \cdot |\vec{b}| \cdot \sin\alpha = S_{\text{параллелограмма}}

|\vec{a} \times \vec{b}| = |\vec{a}| \cdot |\vec{b}| \cdot \sin\alpha = S_{\text{параллелограмма}}

Правило правой руки для векторного произведения

Для определения направления вектора, являющегося результатом векторного произведения, используется правило правой руки:

Расположите правую руку так, чтобы пальцы были направлены вдоль первого вектора
Согните пальцы в направлении ко второму вектору по кратчайшему пути
Отставленный большой палец укажет направление результирующего вектора