Комбинаторика

Комбинаторика — раздел математики, изучающий методы подсчёта количества различных комбинаций объектов, удовлетворяющих определённым условиям. Это фундаментальная дисциплина, имеющая приложения в теории вероятностей, информатике, криптографии и многих других областях.

Историческая справка: Основы комбинаторики были заложены в XVII веке Блезом Паскалем и Пьером де Ферма при изучении азартных игр. Термин "комбинаторика" был введён Готфридом Лейбницем в его работе "Dissertatio de arte combinatoria" (1666).

Основные правила комбинаторики

Правило суммы

Если объект A можно выбрать m способами, а объект B — n способами, причем выбор A и B взаимно исключают друг друга, то выбор «A или B» можно осуществить m + n способами.

📌 пример:

В группе 10 девушек и 12 юношей. Сколькими способами можно выбрать одного представителя группы?

$10 + 12 = 22$ способа.

Правило произведения

Если объект A можно выбрать m способами, и после каждого такого выбора объект B можно выбрать n способами, то выбор «A и B» в указанном порядке можно осуществить m × n способами.

📌 пример:

Сколько различных двузначных чисел можно составить из цифр 1, 2, 3, 4, 5, если цифры не повторяются?

Первую цифру можно выбрать 5 способами, вторую — 4 способами: $5 \times 4 = 20$ чисел.

Основные комбинаторные конфигурации

Перестановки

Комбинации из n элементов, которые отличаются только порядком расположения элементов.

P_n = n!

📌 пример:

Сколькими способами можно расставить 5 книг на полке?

$P_5 = 5! = 1 \times 2 \times 3 \times 4 \times 5 = 120$ способов.

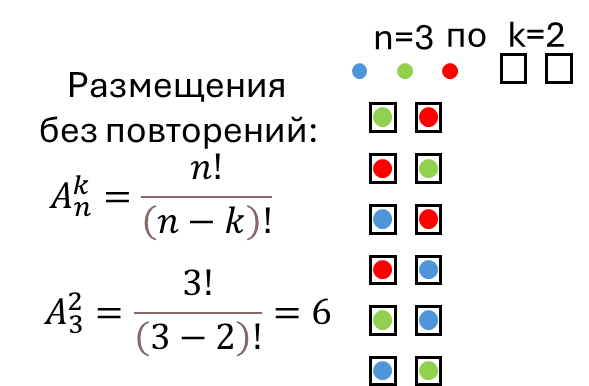
Размещения

Упорядоченные наборы из k элементов, выбранных из n различных элементов.

A_n^k = \frac{n!}{(n-k)!}

📌 пример:

Сколькими способами можно выбрать председателя и секретаря из 10 человек?

$A_{10}^2 = \frac{10!}{8!} = 10 \times 9 = 90$ способов.

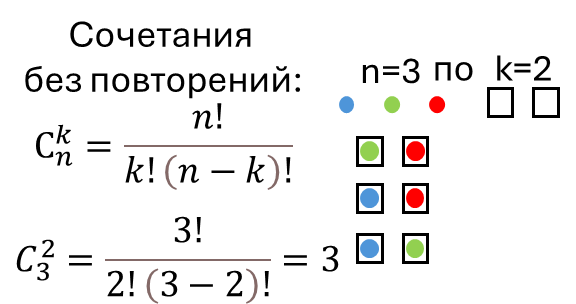
Сочетания

Неупорядоченные наборы из k элементов, выбранных из n различных элементов.

C_n^k = \frac{n!}{k!(n-k)!}

📌 пример:

Сколькими способами можно выбрать 2 дежурных из 5 человек?

$C_5^2 = \frac{5!}{2!3!} = \frac{120}{2 \times 6} = 10$ способов.

Комбинаторика с повторениями

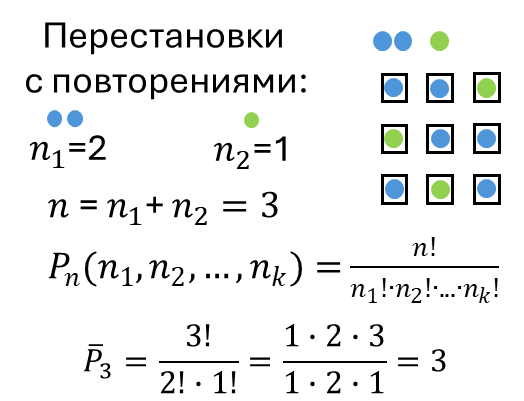
Перестановки с повторениями

Комбинации из n элементов, среди которых есть одинаковые.

P_n(n_1, n_2, ..., n_k) = \frac{n!}{n_1! \cdot n_2! \cdot ... \cdot n_k!}

P_n(n_1, n_2, ..., n_k) = \frac{n!}{n_1! \cdot n_2! \cdot ... \cdot n_k!}

📌 пример:

Сколько различных слов можно составить из букв слова "МАМА"?

Всего 4 буквы: М повторяется 2 раза, А повторяется 2 раза: $P_4(2,2) = \frac{4!}{2! \cdot 2!} = \frac{24}{4} = 6$ слов.

Размещения с повторениями

Упорядоченные наборы из k элементов, выбранных из n различных элементов, причем каждый элемент может повторяться.

\overline{A}_n^k = n^k

📌 пример:

Сколько различных трёхзначных кодов можно составить из цифр 0-9?

На каждой позиции может быть любая из 10 цифр: $\overline{A}_{10}^3 = 10^3 = 1000$ кодов.

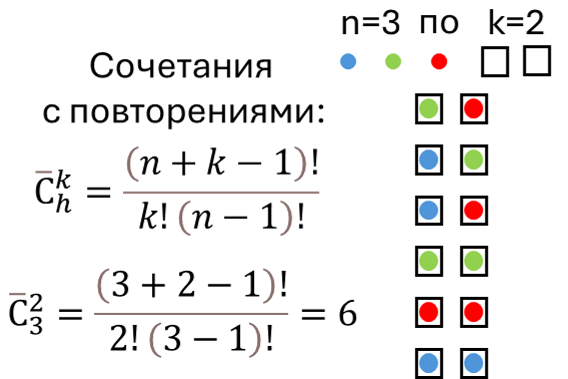
Сочетания с повторениями

Неупорядоченные наборы из k элементов, выбранных из n различных элементов, где элементы могут повторяться.

\overline{C}_n^k = C_{n+k-1}^k = \frac{(n+k-1)!}{k!(n-1)!}

📌 пример:

Сколькими способами можно купить 3 пирожных, если в магазине 4 вида пирожных?

$\overline{C}_4^3 = C_{4+3-1}^3 = C_6^3 = \frac{6!}{3!3!} = 20$ способов.

Бином Ньютона и свойства сочетаний

(a + b)^n = \sum_{k=0}^{n} C_n^k a^{n-k} b^k

Основные свойства сочетаний

$C_n^k = C_n^{n-k}$ (симметрия)
$C_n^k = C_{n-1}^k + C_{n-1}^{k-1}$ (рекуррентное соотношение)
$C_n^0 + C_n^1 + ... + C_n^n = 2^n$
$C_n^0 - C_n^1 + ... + (-1)^n C_n^n = 0$

Треугольник Паскаля

Числа $C_n^k$ можно расположить в виде треугольника, где каждое число равно сумме двух чисел над ним.

Решение комбинаторных задач

Алгоритм решения комбинаторных задач

Определить тип комбинаторной конфигурации (перестановки, размещения, сочетания)
Проверить, есть ли повторения элементов
Определить, важен ли порядок элементов
Выбрать соответствующую формулу
Вычислить результат

📌 пример задачи:

Сколькими способами можно распределить 5 различных подарков между 3 детьми, если каждый ребенок может получить любое количество подарков?

Каждый подарок можно отдать любому из 3 детей: $3^5 = 243$ способа.

Связь с теорией вероятностей

Комбинаторика является фундаментом теории вероятностей. Классическое определение вероятности события основано на подсчете количества благоприятных и всех возможных исходов.

P(A) = \frac{m}{n}

где m — количество благоприятных исходов, n — количество всех возможных исходов

📌 пример: Вероятность вытащить двух тузов из колоды 36 карт: $P = \frac{C_4^2}{C_{36}^2} = \frac{6}{630} = \frac{1}{105}$

Практическое применение

Информатика и программирование

Анализ алгоритмов и сложности
Генерация комбинаторных объектов
Криптография и теория кодирования
Оптимизация баз данных

Теория вероятностей и статистика

Расчет вероятностей событий
Комбинаторные методы в статистике
Планирование экспериментов
Анализ комбинаторных схем

Экономика и бизнес

Анализ инвестиционных портфелей
Оптимизация логистических маршрутов
Планирование производства
Анализ рисков

Биология и генетика

Анализ генетических комбинаций
Исследование белковых структур
Филогенетический анализ
Биоинформатика

Теория вероятностей

Введение в теорию вероятностей

Теория вероятностей — раздел математики, изучающий закономерности случайных явлений и событий. Возникла в XVII веке из азартных игр и развилась в мощный инструмент для анализа неопределенности в науке, технике и экономике.

Исторический факт: Основы теории вероятностей заложили Блез Паскаль и Пьер де Ферма в переписке 1654 года, решая задачи, связанные с азартными играми.

Основные понятия

Событие — любой исход или результат эксперимента. События могут быть:

Достоверное — событие, которое обязательно произойдет
Невозможное — событие, которое не может произойти
Случайное — событие, которое может произойти или не произойти
Элементарное — событие, которое нельзя разложить на более простые

Вероятность — числовая характеристика возможности наступления события. Измеряется от 0 (невозможное событие) до 1 (достоверное событие). Вероятность невозможного события равна 0.

Аксиомы вероятности:
1. P(A) ≥ 0 для любого события A
2. P(Ω) = 1 (вероятность достоверного события равна 1)
3. P(A∪B) = P(A) + P(B) для несовместных событий

Классификация событий

Несовместные и совместные события

Несовместные события — события, которые не могут произойти одновременно в одном испытании.

Совместные события — события, которые могут произойти одновременно в одном испытании.

📌 пример: При бросании игральной кости:
• Выпадение четного (2,4,6) и нечетного (1,3,5) — несовместные события
• Выпадение числа больше 4 (5,6) и четного числа (2,4,6) — совместные события (число 6 удовлетворяет обоим условиям)

Независимые и зависимые события

Независимые события — события, появление одного из которых не влияет на вероятность появления другого.

Зависимые события — события, появление одного из которых влияет на вероятность появления другого.

📌 пример:
• Два последовательных броска монеты — независимые события
• Последовательное извлечение двух карт из колоды без возвращения — зависимые события (состав колоды меняется)

Определения вероятности

Классическое определение

P(A) = \frac{m}{n}

где m — число благоприятных исходов, n — общее число равновозможных исходов.

📌 пример: Вероятность вытащить туза из колоды в 36 карт: $P = \frac{4}{36} = \frac{1}{9}$

Геометрическая вероятность

P(A) = \frac{\text{мера области } A}{\text{мера всей области}}

Используется, когда исходы эксперимента можно представить как точки в некоторой области.

📌 пример: Вероятность попадания точки в интервал [2; 5] на отрезке [0; 10]: $P = \frac{5 - 2}{10 - 0} = 0.3$

Теоремы теории вероятностей

Теорема сложения вероятностей

Для несовместных событий:

P(A \cup B) = P(A) + P(B)

📌 пример (несовместные события):

В колоде 36 карт. Какова вероятность вытащить туза или короля? Эти события несовместны — карта не может быть одновременно тузом и королём.

P(\text{туз}) = \frac{4}{36} = \frac{1}{9}

P(\text{король}) = \frac{4}{36} = \frac{1}{9}

Итог:

P(\text{туз} \cup \text{король}) = \frac{1}{9} + \frac{1}{9} = \frac{2}{9}

P(\text{туз}) = \frac{4}{36} = \frac{1}{9}

P(\text{король}) = \frac{4}{36} = \frac{1}{9}

Итог:

P(\text{туз} \cup \text{король}) = \frac{1}{9} + \frac{1}{9} = \frac{2}{9}

Для совместных событий:

P(A \cup B) = P(A) + P(B) - P(A \cap B)

P(A \cup B) = P(A) + P(B) - P(A \cap B)

📌 пример (совместные события):

В колоде 36 карт. Какова вероятность вытащить черву или туза? Эти события совместны — может быть туз червей.

P(\text{черва}) = \frac{9}{36} = \frac{1}{4}

P(\text{туз}) = \frac{4}{36} = \frac{1}{9}

P(\text{туз червей}) = \frac{1}{36}

Итог:

P = \frac{1}{4} + \frac{1}{9} - \frac{1}{36} = \frac{1}{3}

Итог:

P = \frac{1}{4} + \frac{1}{9} - \frac{1}{36} = \frac{9+4-1}{36} = \frac{12}{36} = \frac{1}{3}

Теорема умножения вероятностей

Для независимых событий:

P(A \cap B) = P(A) \cdot P(B)

📌 пример (независимые события):

Подбрасываем монету и бросаем игральную кость. Какова вероятность, что выпадет орёл и шестёрка? Эти события независимы — результат монеты не влияет на кость.

P(\text{орёл}) = \frac{1}{2}

P(\text{шестёрка}) = \frac{1}{6}

Итог:

P = \frac{1}{2} \times \frac{1}{6} = \frac{1}{12}

Для зависимых событий:

P(A \cap B) = P(A) \cdot P(B|A)

📌 пример (зависимые события):

В урне 5 шаров: 3 синих и 2 красных. Вынимаем два шара подряд без возвращения. Какова вероятность, что оба шара синие?

P(\text{1-ый с-й}) = \frac{3}{5}

P(\text{2-ой с-й | 1-ый с-й}) = \frac{2}{4} = \frac{1}{2}

Итог:

P = \frac{3}{5} \times \frac{1}{2} = \frac{3}{10} = 0.3

P(\text{первый синий}) = \frac{3}{5}

P(\text{второй синий | первый синий}) = \frac{2}{4} = \frac{1}{2}

Итог:

P = \frac{3}{5} \times \frac{1}{2} = \frac{3}{10} = 0.3

Формула Бернулли

P_n(k) = C_n^k \cdot p^k \cdot q^{n-k}

где $C_n^k = \frac{n!}{k!(n-k)!}$ — число сочетаний, p — вероятность успеха в одном испытании, q = 1-p — вероятность неудачи.

📌 пример: Вероятность, что орел выпадет ровно 3 раза при 5 бросках:
$P_5(3) = C_5^3 \cdot \left(\frac{1}{2}\right)^3 \cdot \left(\frac{1}{2}\right)^2 = 10 \cdot \frac{1}{8} \cdot \frac{1}{4} = \frac{10}{32} = 0.3125$

Применение: Формула Бернулли используется для вычисления вероятности определенного числа успехов в серии независимых испытаний с постоянной вероятностью успеха.

Формула полной вероятности и Байеса

Формула полной вероятности

P(A) = \sum_{i=1}^n P(H_i) \cdot P(A|H_i)

Если события H₁, H₂, ..., Hₙ образуют полную группу попарно несовместных событий.

📌 Пример:

На фабрике 2 цеха производят лампочки. 1-й цех — 60%, 2-й цех — 40%. Брак в 1-м цехе — 3%, во 2-м — 5%. Какова вероятность, что случайно выбранная лампочка бракованная?

H₁:лампочка из 1-го цеха, P(H₁) = 0.6

H₂:лампочка из 2-го цеха, P(H₂) = 0.4

A:лампочка бракованная

P(A|H_1) = 0.03

P(A|H_2) = 0.05

По формуле полной вероятности:

P(A) = 0.6 \times 0.03 + 0.4 \times 0.05 = 0.038

P(A) = 0.6 \times 0.03 + 0.4 \times 0.05 = 0.038

Вероятность брака: 3.8%

Формула Байеса

P(H_i|A) = \frac{P(H_i) \cdot P(A|H_i)}{\sum_{j=1}^n P(H_j) \cdot P(A|H_j)}

P(H_i|A) = \frac{P(H_i) \cdot P(A|H_i)}{\sum_{j=1}^n P(H_j) \cdot P(A|H_j)}

Позволяет переоценить вероятности гипотез после получения новой информации (апостериорные вероятности).

📌 Пример (продолжение):

Лампочка оказалась бракованной. Какова вероятность, что она произведена в 1-м цехе?

Используем результат из предыдущего примера:

P(A) = 0.038

P(H_1) = 0.6

P(A|H_1) = 0.03

По формуле Байеса:

P(H_1|A) = \frac{0.6 \times 0.03}{0.038} = \frac{0.018}{0.038} \approx 0.474

P(H_1|A) = \frac{0.6 \times 0.03}{0.038} = \frac{0.018}{0.038} \approx 0.474

Интерпретация:

До проверки: P(H₁) = 0.6 (60%)

После проверки: P(H₁|A) ≈ 0.474 (47.4%)

Зная, что лампочка бракованная, вероятность её производства в 1-м цехе уменьшилась с 60% до 47.4%.

Практическое применение (медицинский тест)

Задача: Тест на заболевание имеет точность 95% (если человек болен, тест положительный с вероятностью 0.95; если здоров — отрицательный с вероятностью 0.95). Заболевание встречается у 1% населения. Человек получил положительный результат теста. Какова вероятность, что он действительно болен?

1. Формула полной вероятности:

H_1: \text{болен}, P(H_1) = 0.01

H_2: \text{здоров}, P(H_2) = 0.99

P(\text{+}|H_1) = 0.95

P(\text{+}|H_2) = 0.05

P(+) = 0.01 \times 0.95 + 0.99 \times 0.05 = 0.059

P(+) = 0.01 \times 0.95 + 0.99 \times 0.05 = 0.059

2. Формула Байеса:

P(H_1|+) = \frac{0.01 \times 0.95}{0.059} \approx 0.161

Вывод: Даже при положительном результате теста вероятность реального заболевания всего ~16.1%. Это показывает важность учета базовой распространенности заболевания.

Практическое применение теории вероятностей

В науке и технике

Статистическая физика — изучение поведения больших ансамблей частиц
Квантовая механика — вероятностная интерпретация волновой функции
Теория информации — вычисление энтропии и пропускной способности каналов
Надежность технических систем — расчет вероятностей отказов
Генетика — предсказание наследования признаков

В повседневной жизни

Страхование — расчет страховых премий и рисков
Медицина — оценка эффективности лечения и диагностические тесты
Финансы — оценка инвестиционных рисков и управление портфелем
Спортивные ставки — расчет вероятностей исходов спортивных событий
Искусственный интеллект — байесовские сети и машинное обучение

Интересные факты о теории вероятностей

Парадокс Монти Холла

Известная вероятностная задача, в которой игрок должен выбрать одну из трех дверей. После открытия одной из дверей без приза, игроку предлагается изменить свой выбор. Вероятность выигрыша увеличивается с 1/3 до 2/3 при смене выбора.

Закон больших чисел

При увеличении числа испытаний среднее арифметическое результатов стремится к математическому ожиданию (ожидаемое значение случайной величины). Это объясняет, почему казино всегда в выигрыше в долгосрочной перспективе, несмотря на случайные выигрыши игроков.